Cell Splitting and Cost Function
I am wondering about cost function applied to the linking between two cells in successive frames in time-lapse images. Following will be the “writing and wondering” practice.
The most simplest way to calculate the cost for linking two cells is the Nearest Neighbor method.
If we have a cell in tth frame at <jsm>(x_{t}, y_{t})</jsm> and another cell in t+1th frame at <jsm>(x_{t+1}, y_{t+1})</jsm>, then the cost function for the nearest neighbor would be
<jsmath> Cost=((x_{t+1}-x_{t})^{2}) + (y_{t+1}-y_{t})^{2}) </jsmath>
which is the distance between two. This works well if cells are sparsely located, clearly segmentable and time-lapse sequence was taken with enough time resolution. Modifications are generally made to such cost function since the real experimental results are always not in such ideal condition.
One problem I have is this: cells are artificially divided by watershed algorithm during segmentation (over-segmented). I want to get rid of such from cell-cell linking to have a good tracking results. How do I do it? I need to add more term in the cost function in order to add additional cost for liking such over-segmented cells (I would rather like to jump over such).
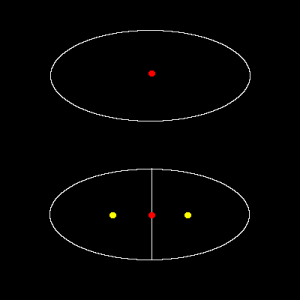
Figure shown below illustrates the situation.
Here, I could maybe estimate the displacement (red dot to one of yellow dots) due to artificial splitting as a half of the radius of original cell, since the daughter cells would be approximately half the size of the original. Then approximately <jsm>1/2 radius</jsm> of displacement could maybe used as an indicator of “wrongly linked” due to over-segmentation. But what happens, if cells are actually moving at a speed of half the radius displacement per time frame?
Of course, we could take the time series with a time resolution that is high enough to capture cells before it move half of its radius. This actually is true, cells do not move much per frame in the case of sequence I am dealing with.
Just to think about more general way, we could also estimate the abnormality from changes in the cell size (in 2D, this would be cell area). In the example case above, cell area becomes half by over-segmentation. That seems to be clear, but how could we include this area change phenomena in the cost function?
The additional cost could be designed as follows:
First, I define that decrease in the area by half the area in time point t would be a cost of the maximum displacement value. This value could be estimated from other source, such as previous studies or manual tracking of cells. Many tracking software introduces this value, to decrease calculation cost and also avoid false linkage. Here, we call this value <jsm>d_{max}</jsm>. Then we should have a factor a that converts area decrease by half to the maximum distance: <jsmath> \displaylines{ d_{max} = a(\frac{A_{t}}{2}) \cr a = \frac{2d_{max}}{A_{t}} } </jsmath> where <jsm>A_{t}</jsm> is the area at time point t. Updated cost function will then be <jsmath> Cost=((x_{t+1}-x_{t})^{2}) + (y_{t+1}-y_{t})^{2}) + \frac{2d_{max}}{A_{t}}(A_{t} - A_{t+1}) </jsmath>
Now, considering that the area in t+1th could be larger (cells might artificially fuse due to under-segmentation), we could also set positive cost for that. <jsmath> Cost=((x_{t+1}-x_{t})^{2}) + (y_{t+1}-y_{t})^{2}) + \frac{2d_{max}}{A_{t}}abs(A_{t} - A_{t+1}) </jsmath>
…newly added term is computationally more efficient in a form <jsmath> 2d_{max}abs(1 - \frac{A_{t+1}}{A_{t}}) </jsmath>
OK, that seems to be a simple solution. Problem with this is that when cell is moving fast, then there could be large area changes as well. Both of these things happening together would cause higher cost. mmm…