CMCI weblog
New Server
This site has migrated to a new server and also now running with the most recent Dokuwiki! You might not recognize this move and upgrade, but this could not have been done with helps and hackings by Agustin Villalba @ IT service. This Dokiwiki web application is running with sqlite3 (Dokuwiki does not deal with sqlite3 normally). Thanks to Agustin!
ISBI 2012, Satellite Meeting

A picture with the ImageJ founder, Wayne Rusband.
A meeting titled “Bioimage analysis software: is there a future beyond ImageJ?” took place in Barcelona between April 31st and May 1st (http://bigwww.epfl.ch/eurobioimaging/). Some key presentations were given by Wayne Rusband, Johannes Schindlin, Curtis Rueden and all the famous developers among ImageJ community and more software such as Icy and BioimageXD.
Wayne talked about how he started developing NIH Image in 1987, with some pictures of initial Apple II machine he was developing with. The software was coded in pascal, and I told him that I started using it in 1993 and was fascinated by the ImageJ macro language. He also informed us with his latest update, pixel inspector that shows the distribution of values in the vicinity of the cursor location.
Intensive discussions on strengthening the community was held as well, mainly in the direction of setting up a core portal and planning periodic meetings.
Two Lectures on Classification and Clustering, April and May
Coupled lectures on Classification and Clustering will be given in the CMCI seminar in April and May. These two approaches have been widely used for screening and system descriptions, but there seems to be more in the future in terms of image processing and analysis, as we have seen in the CMCI seminar in March. For this reason we asked for introduction for these two topics by two experts in the EMBL. Bernd Fischer will give us a lecture on Classification and Machine learning, and Jean-Karim Heriche will give a lecture on cluster analysis.
CMCI seminar Nov. 25, 2011 14:00
There will be talks by Christoph Moehl and Tomoya Kitajima.
Cell Splitting and Cost Function
I am wondering about cost function applied to the linking between two cells in successive frames in time-lapse images. Following will be the “writing and wondering” practice.
The most simplest way to calculate the cost for linking two cells is the Nearest Neighbor method.
If we have a cell in tth frame at <jsm>(x_{t}, y_{t})</jsm> and another cell in t+1th frame at <jsm>(x_{t+1}, y_{t+1})</jsm>, then the cost function for the nearest neighbor would be
<jsmath> Cost=((x_{t+1}-x_{t})^{2}) + (y_{t+1}-y_{t})^{2}) </jsmath>
which is the distance between two. This works well if cells are sparsely located, clearly segmentable and time-lapse sequence was taken with enough time resolution. Modifications are generally made to such cost function since the real experimental results are always not in such ideal condition.
One problem I have is this: cells are artificially divided by watershed algorithm during segmentation (over-segmented). I want to get rid of such from cell-cell linking to have a good tracking results. How do I do it? I need to add more term in the cost function in order to add additional cost for liking such over-segmented cells (I would rather like to jump over such).
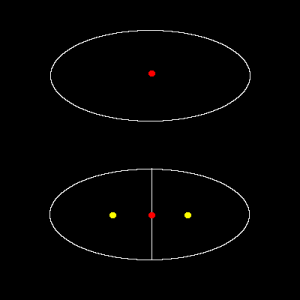
Figure shown below illustrates the situation.
Here, I could maybe estimate the displacement (red dot to one of yellow dots) due to artificial splitting as a half of the radius of original cell, since the daughter cells would be approximately half the size of the original. Then approximately <jsm>1/2 radius</jsm> of displacement could maybe used as an indicator of “wrongly linked” due to over-segmentation. But what happens, if cells are actually moving at a speed of half the radius displacement per time frame?
Of course, we could take the time series with a time resolution that is high enough to capture cells before it move half of its radius. This actually is true, cells do not move much per frame in the case of sequence I am dealing with.
Just to think about more general way, we could also estimate the abnormality from changes in the cell size (in 2D, this would be cell area). In the example case above, cell area becomes half by over-segmentation. That seems to be clear, but how could we include this area change phenomena in the cost function?
The additional cost could be designed as follows:
First, I define that decrease in the area by half the area in time point t would be a cost of the maximum displacement value. This value could be estimated from other source, such as previous studies or manual tracking of cells. Many tracking software introduces this value, to decrease calculation cost and also avoid false linkage. Here, we call this value <jsm>d_{max}</jsm>. Then we should have a factor a that converts area decrease by half to the maximum distance: <jsmath> \displaylines{ d_{max} = a(\frac{A_{t}}{2}) \cr a = \frac{2d_{max}}{A_{t}} } </jsmath> where <jsm>A_{t}</jsm> is the area at time point t. Updated cost function will then be <jsmath> Cost=((x_{t+1}-x_{t})^{2}) + (y_{t+1}-y_{t})^{2}) + \frac{2d_{max}}{A_{t}}(A_{t} - A_{t+1}) </jsmath>
Now, considering that the area in t+1th could be larger (cells might artificially fuse due to under-segmentation), we could also set positive cost for that. <jsmath> Cost=((x_{t+1}-x_{t})^{2}) + (y_{t+1}-y_{t})^{2}) + \frac{2d_{max}}{A_{t}}abs(A_{t} - A_{t+1}) </jsmath>
…newly added term is computationally more efficient in a form <jsmath> 2d_{max}abs(1 - \frac{A_{t+1}}{A_{t}}) </jsmath>
OK, that seems to be a simple solution. Problem with this is that when cell is moving fast, then there could be large area changes as well. Both of these things happening together would cause higher cost. mmm…