April 20, 2010 @EMBL Kota Miura
will be also further added by Sebastian Huet and Christian Tischer

Google Chrome or Firefox (version > 3.6) is recommended for properly viewing math equations.

in vivo protein kinetics could be analyzed in two ways: measuring particular movement or averaged movement. By tracking labeled single protein molecules, it is possible to estimate their diffusion and transport behavior. Single molecule studies of membrane proteins enabled us to analyze how they are organized with their dynamics, through corrals of membrane territory. Motor protein moving along cytoskeletal tracks were analyzed in detail how they convert chemical energy into physical force was only possible by probing their singular movement and steps. While single particle tracking requires high-temporal and spatial resolution setup for analysis, analysis of averaged movement measured through fluorescence intensity dynamics, could be achieved with larger spatial and temporal resolution (typically in micrometer scale).

Here, we focus on one of such averaged movement analysis technique, Fluorescence Recovery After Photobleaching (FRAP). We first start with a simpler case of monitoring averaged movement that does not need to bleach.

Measurement of VSV-G protein exit dynamics

First-order Chemical Reaction

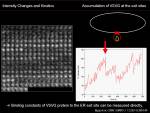
Increase in intensity at observed area could be measured to know the net increase in the protein at that region. To calculate biochemical kinetics, we can apply traditional biochemical kinetics. Example case: Kinetics of VSVG protein accumulation to ER exit site.

<jsmath>{dI(t)\over dt}=k_{on}[VSVG_{free}]- k_{off}[VSVG_{ERES}]</jsmath>

Here,

• <jsm>k_{on}</jsm> is the binding rate of VSVG protein to ER exit site
• <jsm>[VSVG_{free}]</jsm> is the concentration of unbound VSVG protein
• <jsm>k_{off}</jsm> is the dissociation rate of VSVG protein from ER exit site
• <jsm>[VSVG_{ERES}]</jsm> is the density of VSVG protein bound to the ER exit site

During the initial phase of binding, when there is almost no VSVG protein bound to ER exit site, we can approximate the initial speed of the density increase at ERES site depends only on binding reaction and assume <jsm>k_{off}[VSVG_{ERES}]\simeq0</jsm>. Then

<jsmath> {dI(t)\over{dt}}=k_{on}[VSVG_{free}] </jsmath>

Since there are enough free VSVG, we consider that <jsm>[VSVG_{free}]</jsm> is constant, we are able to simply calculate the slope of initial increase of intensity, measure the free VSVG intensity and then calculate <jsm>k_{on}</jsm>.

For details, see Runz et al (2006).

Half-Max t and Mobile/Immobile fraction from FRAP curve

Unlike the example explained above, dynamics of protein are not observable in many cases. Even though proteins are exchanging in system, the flux of protein constituting the system is not evident if the flux is steady and constant (e.g. liver). In such cases, we need to some how experimentally measure the system. One way is FRAP. In FRAP, we bleach some population of fluorescence-labeled protein and evaluate the mobility of the protein. Typically, we use confocal microscopy and bleach fluorescence of small area of the system by short pulse of strong laser beam and measure changes in the fluorescence intensity over time at that bleached spot over time. Detail on these measurement protocol has been presented in Stefan and Yury's talks (link?). Here, we focus on how to analyze the curve we obtained by such measurements.

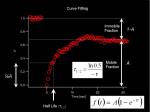
From measured temporal changes in the intensity at the bleached Region of Interest (this curve indeed is the Fluorescence Recovery After Photobleaching, FRAP)

Half Max and Mobile-Immobile fraction
Fitting to Exponential curve

FRAP curve reflects the mobility of proteins. In dilute solution of single protein species, mobility of protein could probably be considered as pure-diffusion. But in many cases, this is not the case. The mobility is affected by the system.

• reaction with other proteins
• geometry of the system, that constrains the mobility
• active transport process

By modeling how the mobility is (generate some hypothesis how the protein mobility is affected in the system), we can set up equation/s to that should describe the FRAP curve. This is done by fitting the theoretical curves to the experimental curves. By evaluating the goodness of fit, we can discuss which models would be the most likely hypothesis.

Currently we have more-or-less standardized protocol to analyze FRAP curve. Starting with simple model of diffusion, we test the fit of different curves and proceed to more complex models. See next section for the protocol.

Maybe Sebastian's flow chart here.

Theoretical curve of the diffusion mediated fluorescence recovery was proposed by Soumpasis (1984) and has been widely used.
<jsmath> f(t)=e^{- \frac{\tau_D}{2t}}\left(I_{0}(\frac{\tau_D}{2t})+I_{1}(\frac{\tau_D}{2t})\right) </jsmath> This theoretical equation assumes:

• 2D
• circular (cylindrical) bleaching

when above equation could be fitted nicely (evaluated by goodness of fit, such as Pearson's coefficient r or gamma-Q value), one could calculate diffusion coeffecient by using the obtained <jsm>\tau_D</jsm> and radius of the circular ROI <jsm>w</jsm>.
<jsmath> D=\frac{w^{2}}{\tau_D} </jsmath>

(almost diffusion)

Protein cluster and fluorescence recovery

Modeling Reaction Dominant recovery

If molecule under study is binding/unbinding with other molecular species, FRAP curve is affected by this interaction. There are two cases on how these two events, diffusion and reaction, are combined in the curve. We could think of two cases.

1. Reaction-dominant recovery Cases when reaction binding rate (meaning “number of molecules that binds to the binding partner per second”) is much lower than the diffusion rate. In such cases, FRAP-bleached field will be become brighter due to diffusion, and then there will be a slower recovery of intensity due to none-bleached fluorescence exchange with the bleached fluorescence. In such cases, we could consider that the recovery curve is dominated by reaction since duration of diffusion-recovery phase and reaction-recovery phase is much shorter for the diffusion-recovery phase, these two phases could be assumed to be separated(call this reaction-dominant or diffusion uncoupled; this section).
2. Reaction-Diffusion Recovery Other cases would be when durations of diffusion-recovery phase and reaction-recovery phase are comparable. Then recovery curve consists of a combination of fluorescence that came in with diffusion, and also by the binding of fluorescence molecule at the FRAP bleached field (“reaction-diffusion” or “diffusion-coupled” see the section below).

For a simple chemical reaction with singular type of interaction, we could again think of the reaction model that was already explained above, the first-order chemical reaction could be modeled as compartment system (see figure right)
<jsmath> \frac {df(t)} {dt} = k_{on}[free] - k_{off}[bound] </jsmath> where

• <jsm>k_{on}</jsm> Binding constant
• <jsm>k_{off}</jsm> Dissociation constant
• <jsm>[free]</jsm> Density of free molecules
• <jsm>[bound]</jsm> Density of bound-molecules

We solve the differential equation <jsmath> f(t)=A(1-e^{- \tau t}) </jsmath> where

• <jsm>\tau = k_{on} + k_{off}</jsm>
• <jsm>A = \frac {k_{on}}{k_{on} + k_{off}}</jsm>

Illustrated view of Fluorescence recovery at immobile binding partner

Modeling fluorescence recovery at immobile binding partner 01

Modeling fluorescence recovery at immobile binding partner 02

Next we modify above model to consider a situation a bit more frequently we see in cell biology. The protein we are analyzing is either freely diffusion in cytoplasm or bound to an immobile structure inside cell. We FRAP at this structure, to know the kinetic constants of the protein against the structure (e.g. microtubule binding protein, structure = microtubule) <jsmath> \frac {df(t)} {dt} = k_{on}[free][s] - k_{off}[bound] </jsmath> where

• <jsm>k_{on}</jsm> Binding constant
• <jsm>k_{off}</jsm> Dissociation constant
• <jsm>[free]</jsm> Density of free molecules
• <jsm>[s]</jsm> Density of immobile binding partner
• <jsm>[bound]</jsm> Density of bound-molecules

Since [s] is immobile and constant during experiment, we define <jsm>k*_{on}</jsm> as <jsmath> k*_{on}=k_{on}[s] </jsmath> in addition, density of free molecule in cytoplasm is almost constant so we assume <jsm>[free] = F</jsm> and does not change. We then solve <jsmath> \frac {df(t)} {dt} = k*_{on}F - k_{off}[bound] </jsmath> We get <jsmath> f(t)=1-Ce^{- \tau t} </jsmath> where

• <jsm>\tau = k_{off}</jsm>

… note that the recovery now only depends on <jsm>k_{off}</jsm>

Diffusion-Reaction Combined Model

<jsmath> \frac{\partial [free]}{\partial t} = D_{free} \nabla ^2[free]-k_{on}[free][s]+k_{off}[bound] </jsmath> <jsmath> \frac{\partial [s]}{\partial t} = D_s \nabla ^2[s]-k_{on}[free][s]+k_{off}[bound] </jsmath> <jsmath> \frac{\partial [bound]}{\partial t} = D_{bound} \nabla ^2[bound]+k_{on}[free][s]-k_{off}[bound] </jsmath>

Since

• [s] is constant and immobile
  • <jsm>k*_{on} = k_{on}[s]</jsm>
  • <jsm>\frac{\partial [s]}{\partial t}=0 </jsm>
  • bound molecules do not diffuse so <jsm>D_{bound}=0</jsm>

Then we solve only <jsmath> \frac{\partial [free]}{\partial t} = D_{free} \nabla ^2[free]-k*_{on}[free]+k_{off}[bound] </jsmath> <jsmath> \frac{\partial [bound]}{\partial t} = k_{on}[free][s]-k_{off}[bound] </jsmath>

We did not talk about this issue in the course, but there is another factor that could interfere with recovery curve in vivo: active transport. There is some trial on including issue by Hallen and Endow (2009).

• ImageJ Plugins: Two available ImageJ plugins for FRAP does intensity measurement and normalization. Fitting module is not implemented.
  • FRAP analysis
  • FRAP Norm|
  • There is a good step-by-step protocol for measurements and analysis using MBF ImageJ bundle. You need to download the bundle from the linked site, and also ask for some plugins directly by email.
• FRAP analysis (EMBL)
  • Import data output from Zeiss, Leica, Olympus measurements and do FRAP fitting.
• MIPAV
  • Does measurement and fitting. Sprague et al. (2004) Reaction-Diffusion Full model is implemented.

Requires your own coding, customization

Sprague et. al. (explained above) is an example case of analytically solving the model for the fitting.

Image based simulation with ODE solver

Tropical

• Numerical analysis based on ODE. Spatial context.

General Solvers

• Berkley Madonna
  • Joel and Sebastian uses this software for fitting ODE.
• MATLAB

One of Particle Simulator, Smodldyn

Custom tool for Particle Simualation

Particle Simulation Packages

• Smoldyn
• GridCell
• MCell

Reviews, Protocols and textbooks

• McNally, J.G. (2008) Quantitative FRAP in analysis of molecular binding dynamics in vivo. Methods in Cell Biology 2008;85:329-51
  
  • step-by-step protocol for analyzing FRAP. Flow chart for determining recovery model is useful.
• Sprague, B. L. and McNally, J. G.(2005). FRAP analysis of binding: proper and fitting. Trends Cell Biol 15, 84-91.
• Phair, R. D., Gorski, S. A. and Misteli, T. (2004). Measurement of dynamic protein binding to chromatin in vivo, using photobleaching microscopy. Methods Enzymol 375, 393-414.
  • Already a bit of out-dated but “Double normalization” introduced in this protocol is widely used.
• Jacquez, J. A. (1972). Compartmental analysis in biology and medicine: Elsevier
  • If you want to study basics about calculation of kinetics.

Research Papers

• Soumpasis, D. M. (1983). Theoretical analysis of fluorescence photobleaching recovery experiments. Biophys J 41, 95-7.
  • Fitting 2D diffusion, circular ROI bleaching.
• Sprague, B. L., Pego, R. L., Stavreva, D. A. and McNally, J. G. (2004). Analysis of binding reactions by fluorescence recovery after photobleaching. Biophys J 86, 3473-95.
  • details on analytical approach for full diffusion-reaction model.
• Sbalzarini, I.F., A. Hayer, A. Helenius, and P. Koumoutsakos. (2006) Simulations of (an)isotropic diffusion on curved biological surfaces. Biophys J. 90:878-85.
• Sbalzarini, I.F., A. Mezzacasa, A. Helenius, and P. Koumoutsakos. (2005) Effects of organelle shape on fluorescence recovery after photobleaching. Biophys J. 89:1482-92.
  • papers which revealed that spatial and geometrical factors are very important for the interpretation and analysis of FRAP curves.
• Beaudouin, J., Mora-Bermudez, F., Klee, T., Daigle, N. & Ellenberg, J.(2006) Dissecting the contribution of diffusion and interactions to the mobility of nuclear proteins. Biophys J. 2006 Mar 15;90(6):1878-94.
  • full reaction-diffusion fitting by numerical approach, with spatial context
• Ulrich M, Kappel C, Beaudouin J, Hezel S, Ulrich J, Eils R.(2006)Tropical–parameter estimation and simulation of reaction-diffusion models based on spatio-temporal microscopy images. Bioinformatics. 22(21):2709-10