Photobleaching Correction -3D time series
There are several IJ tools available for 2D time series bleaching correction, but seems not with 3D:
2D-t tools:
-
- IJ maco, correction by ratio against the first frame. This is basically same as what is proposed in IJ-maillist by Stephan Preibisch.
- “int_ratio=picsum1/picsum”
-
- Phair's double normalization method. Dependent on ratio, similar to the above, but can specify reference area (if my understanding is correct).
-
- proposes two ways,
- conceptually similar to above two: estimate the correction ratio. But this is done by fitting exponential decay curve and use decay parameter.
- <jsm> I_c(t) = I(t) / exp^{-\tau t}</jsm>
- use “enhance contrast”. framewise Histogram streching.
Among these, exponential decay method is theoretically clean (but in practice, timeseries are not teoretical…).
Anycase, there should be 3D-t bleach correction tool (and I need it NOW). I might make some quick solution using two methods, one using division of first frame and the other with exponential fitting.
By the way, bleaching corrected images cannot basically be used for intensity quantification (FRAP, on the other hands, correct bleaching after measuring the raw image). If you are analyzing shapes or positions, no problem for quantification.
here is the “ratio” version:
macro "Bleach Corection 3D-t by ratio"{
run("Duplicate...", "title=bleach_corrected duplicate");
getDimensions(width, height, channels, slices, frames);
if (frames == 1) {
uslices = getNumber("how many z slices/timepoint?", 1);
if ((slices%uslices) !=0) exit("that slice number dows not match with the current stack");
frames = slices / uslices;
}
tIntA = newArray(frames);
setBatchMode(true);
for(i=0; i<frames; i++){
startf = (i*slices)+1;
endf = (i+1)*slices;
op ="start="+startf+" stop="+endf+" projection=[Sum Slices]";
run("Z Project...", op);
//print(op);
getRawStatistics(nPixels, mean);
if (i==0) tIntA[i] = mean;
else tIntA[i] = mean/tIntA[0];
close();
}
setBatchMode("exit and display");
tIntA[0] =1;
for(i=0; i<frames; i++){
for(j=0; j<slices; j++){
curframe = i*slices + j+1;
setSlice(curframe);
//print("frame"+curframe + " factor" + tIntA[i]);
op = "value="+tIntA[i]+" slice";
run("Divide...", op);
}
print("time point:"+i+1 + " factor" + tIntA[i]);
}
}
Before Correction (each row is a time point, with 8 z-slices)
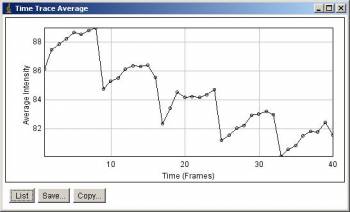
 Average intensity along stack slices. 5 peaks corresponds to 5 time points.
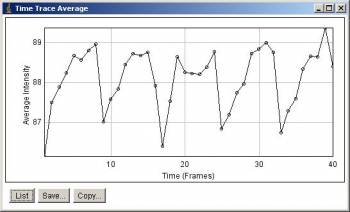
Average intensity along stack slices. 5 peaks corresponds to 5 time points.